В мире анализа временных рядов, где мы пытаемся понять и предсказать поведение данных, изменяющихся во времени, одним из ключевых понятий является гетероскедастичность. Если говорить простыми словами, это ситуация, когда разброс (или волатильность) данных не остается постоянным на протяжении всего периода наблюдения. Разберемся, что такое гетероскедастичность, подробнее.
Почему это важно?
Большинство классических статистических моделей, используемых для анализа временных рядов, основаны на предположении о гомоскедастичности, то есть о постоянстве дисперсии (разброса) ошибок. Если это предположение нарушается, то есть присутствует гетероскедастичность, то результаты таких моделей могут быть искажены. Это может привести к:
- Неверным выводам о статистической значимости. Мы можем ошибочно считать, что какой-то фактор влияет на временной ряд, хотя на самом деле это лишь следствие меняющейся волатильности.
- Неточным прогнозам. Модели, игнорирующие гетероскедастичность, будут хуже предсказывать будущие значения, особенно в периоды высокой волатильности.
- Неэффективным оценкам параметров. Оценки коэффициентов моделей могут быть смещенными или иметь некорректные стандартные ошибки.
Как обнаружить гетероскедастичность?
Существуют различные методы для обнаружения гетероскедастичности:
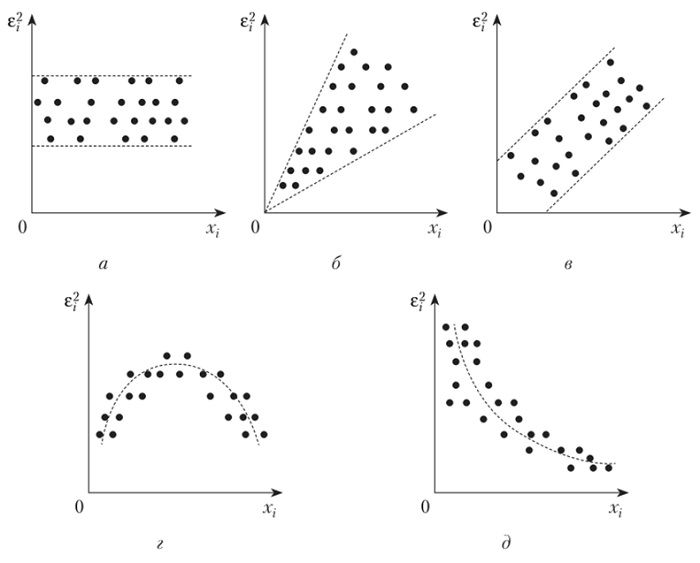
- Визуальный анализ. Построение графиков временного ряда и его остатков может дать первое представление о наличии или отсутствии гетероскедастичности. Если остатки группируются в “полосы” с разной шириной, это явный признак.
- Статистические тесты. Существуют специальные тесты, такие как тест Бреуша-Пагана, тест Уайта или тест Голдфелда-Квандта, которые позволяют формально проверить гипотезу о гомоскедастичности.
- Анализ автокорреляции остатков. Изучение автокорреляционной функции остатков может выявить закономерности, связанные с меняющейся волатильностью.
Что делать, если гетероскедастичность обнаружена?
Если гетероскедастичность присутствует, необходимо использовать специальные модели, которые учитывают это явление. Наиболее распространенными подходами являются:
- Модели ARCH (Autoregressive Conditional Heteroskedasticity) и GARCH (Generalized Autoregressive Conditional Heteroskedasticity). Эти модели специально разработаны для моделирования и прогнозирования меняющейся во времени дисперсии. Они позволяют предсказывать, как волатильность будет меняться в будущем, основываясь на прошлых значениях.
- Взвешенные методы наименьших квадратов (WLS). В этом подходе наблюдениям с меньшей дисперсией придается больший вес, что помогает получить более точные оценки параметров.
- Робастные стандартные ошибки. Использование робастных стандартных ошибок позволяет получить корректные оценки статистической значимости даже при наличии гетероскедастичности.
Понимание и учет гетероскедастичности временных рядов является критически важным для построения надежных моделей и получения достоверных результатов в анализе данных. Стоит глубже изучить понятие, ведь это возможность предотвращать ошибки!